LRU

Abstract

Recurrent Neural Networks(RNNs)는 긴 시퀀스에서 빠른 추론을 제공하지만 학습 속도가 느리고 최적화가 어렵다. 최근 Deep state-space models(SSMs)은 긴 시퀀스 모델링에서 뛰어난 성능과 빠른 훈련 속도를 보여주었다. 이 논문에서는 표준 신호 전파 기법을 통해 깊은 RNN의 성능을 개선하고 학습 속도를 높일 수 있음을 보여준다. 이를 위해 RNN의 회귀를 선형화하고 대각화하며, 매개변수화와 초기화를 개선하고, 순방향 전파를 적절히 정규화하는 방법을 사용하였다. 결과적으로 Long Range Arena 벤치마크에서 SSMs와 동일한 성능과 효율성을 갖춘 ‘Linear Recurrent Unit’을 제안한다.

Introduction

순환 신경망(RNNs)은 딥러닝 초기부터 순차적 데이터 모델링에 중요한 역할을 해왔으나, 기울기 소실 및 기울기 폭주 문제로 인해 학습이 어렵고 장기 종속성 학습에 한계가 있다. 이를 해결하기 위해 LSTM, GRU 등 여러 기술이 개발되었지만, 여전히 계산이 순차적이어서 최적화가 느리고 확장하기 어렵다.

최근 Transformer 모델은 순차 데이터 처리에서 큰 성공을 거두었으며, RNNs보다 학습 시 확장성과 병렬화가 용이하다. 그러나 Transformer는 계산 및 메모리 비용이 시퀀스 길이에 따라 제곱적으로 증가하기 때문에 긴 시퀀스에 대해 비용이 많이 들 수 있다. 반면, RNNs는 시퀀스 길이에 선형적으로 비례하여, 비교적 짧은 시퀀스에서는 추론 속도가 더 빠를 수 있다.

Gu et al. (2021a)은 S4 모델을 소개하였다. S4는 deep state-space model(SSM)로, Long Range Arena (LRA) 벤치마크에서 뛰어난 성능을 보인다. S4는 연속 시간 선형 상태공간 모델에서 영감을 받았으며, attention 레이어의 $O(L^2)$ 병목 현상을 숨겨진 상태를 통해 극복한다. 이 모델은 RNN처럼 레이어를 전개하여 추론 시 효율적이며, 시간 차원에서 선형적이어서 학습 중 병렬화가 용이하다.

S4 모델은 추론 시 RNN과 유사하지만, 학습 중에는 미분 방정식의 연속 시간 시스템을 이산화하여 매개변수화하고, 다항식 투영 이론에 기반한 초기화를 사용한다. 그러나 후속 연구에서는 이러한 초기화가 성능에 필수적이지 않으며, 이론과 다른 이산화 규칙이 더 나은 성능을 낼 수 있다고 제안하였다. 따라서, S4의 독특한 특성과 그 단순화 가능성은 아직 명확하지 않다.

RNN과 deep state-space model(SSMs)의 유사성을 바탕으로, 긴 거리 추론을 위한 깊은 아키텍처에서 RNN의 성능과 한계를 연구하여 그 기본 메커니즘을 이해하는 것이 이 연구의 주요 목표이다.

“deep state-space model(SSMs)의 성능과 효율성을 deep RNN으로 맞출 수 있을까?”"

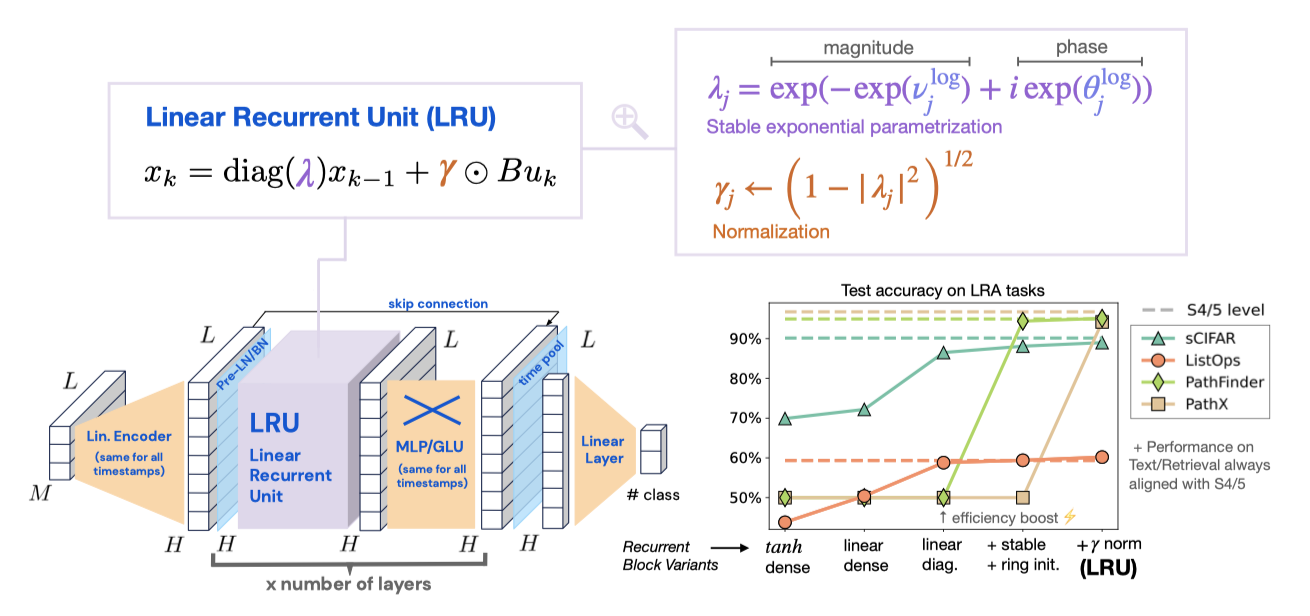
기본 RNN에 작은 변화를 주어 S4와 같은 deep state-space model의 성능과 효율성을 달성할 수 있음을 보여준다. 이 새로운 RNN 모델을 ‘Linear Recurrent Unit’ 또는 줄여서 LRU라고 부른다.

Main Steps. 이 논문에서는 성능이 뛰어나고 효율적인 RNN 모델을 만드는 주요 단계를 설명하며, 새로운 관점과 신중한 분석을 통해 깊은 RNN의 훈련과 초기화에서의 도전 과제와 최선의 방법을 제시한다.

Linear Recurrences. SSM 레이어를 기본 RNN 레이어로 교체하면 LRA에서 성능이 크게 떨어지지만, 선형 회귀를 사용하면 테스트 정확도가 향상된다. 선형 RNN과 비선형 MLP 블록을 조합하면 비선형 시퀀스 매핑을 효과적으로 모델링할 수 있으며, 비선형성을 제거하면 기울기 문제를 제어하고 학습을 병렬화할 수 있다. 이러한 점이 깊은 SSM의 성공을 부분적으로 설명한다.
Complex Diagonal Recurrent Matrices. 밀집 선형 RNN 레이어는 대각 형태로 재매개변수화할 수 있으며, 이는 학습 속도를 크게 향상시킨다. 이러한 접근은 이전 SSM들에서도 사용되었으며, 선형 RNN 레이어의 효율성도 개선한다.
Stable Exponential Parameterization. 대각 순환 행렬에 지수 매개변수를 사용하면 학습 중 안정성을 보장하고 긴 거리 추론을 촉진할 수 있음을 보여준다. 초기화 시 순환 레이어의 고유값 분포가 긴 거리 추론의 성능을 결정한다.
Normalization. 긴 거리 의존성이 있는 작업에서 순방향 전파의 활성화 정규화가 중요하다고 설명하며, 이 수정으로 RNN이 LRA 벤치마크에서 깊은 SSM과 같은 성능을 발휘할 수 있음을 보여준다. 또한, 이 정규화가 S4의 이산화 구조와 어떻게 연결되는지 설명한다.

이 논문에서는 깊은 선형 순환 유닛(LRU) 아키텍처와 각 단계의 성능 영향을 요약한다. 주된 목적은 S4 모델의 성능을 초월하는 것이 아니라, 적절히 초기화된 단순 RNN이 긴 거리 추론에서 강력한 성능을 발휘할 수 있음을 보여주는 것이다.

Preliminaries

RNNs과 SSMs의 주요 구성 요소를 비교하고, 방법론과 실험 설정을 설명한다.

Recap of recurrent block structures

이 논문에서는 Vanilla RNNs와 최신 S4 계열 심층 SSMs의 주요 차이점을 중심으로 주요 아키텍처 구성 요소를 비교한다.

RNN Layer. $(u_1, u_2, \ldots, u_L)$을 $H$차원 입력 시퀀스라고 할 때, $N$차원의 은닉 상태를 가진 RNN 계층은 학습 가능한 매개변수 $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$, $\mathbf{D}$를 통해 $H_{\text{out}}$ 차원의 출력 시퀀스 $(y_1, y_2, \ldots, y_L)$를 다음과 같이 계산한다:

$$ x_k = \sigma(\mathbf{A}x_{k-1} + \mathbf{B}u_k), y_k = \mathbf{C}x_k + \mathbf{D}u_k $$

여기서 $x_0 = 0$이며, $\sigma$는 주로 $\tanh$나 시그모이드 비선형 함수이다. $\sigma$가 항등 함수이면, 해당 RNN은 선형이다.

S4-like recurrent layer. 이 논문에서는 Gu et al. (2021a)에서 도입된 S4 재귀의 단순화된 버전을 제시한다. 입력 시퀀스 $(u_0, u_1, \ldots, u_{L-1})$는 $\Delta > 0$의 스텝 크기로 샘플링된 연속 시간 신호로 간주되며, 출력 시퀀스 $(y_0, y_1, \ldots, y_{L-1})$도 동일한 방식으로 샘플링된다. 이 모델은 다음과 같은 연속 시간 상태 공간 모델로 표현된다:

$$ {{d}\over{dt}} x_{ct}(t) = \tilde{\mathbf{A}} x_{ct}(t) + \tilde{\mathbf{B}} u_{ct}(t), $$

$$ y_{ct}(t) = \Re[\tilde{\mathbf{C}} x_{ct}(t)] + \tilde{\mathbf{D}} u_{ct}(t), $$

여기서 $\tilde{\mathbf{A}}$는 대각선 형태의 복소수 행렬이며, $\tilde{\mathbf{B}}$, $\tilde{\mathbf{C}}$, $\tilde{\mathbf{D}}$는 복소수 매개변수이다. 이 모델은 연속 시간 특성을 무시하면 위 식과 비교했을 때 계산이 선형이고, 매개변수가 복소수라는 점이 차별점이다. 학습과 추론을 위해 이 시스템은 ZOH 방법을 사용해 이산화되며, 다음과 같은 형태를 가진다:

$$ x_k = \mathbf{A}x_{k-1} + \mathbf{B}u_k, y_k = \mathbf{C}x_k + \mathbf{D}u_k, $$

여기서 $\mathbf{A} = \exp(\Delta \tilde{\mathbf{A}})$ 등으로 정의된다.

Some key diﬀerences. RNN과 SSM의 주요 차이점은 다음과 같다:

위 식 은 선형이기 때문에 비선형 RNN과 달리 병렬 스캔을 사용해 효율적으로 병렬화할 수 있다.
$A$와 $B$ 행렬은 이산화에 의해 규정된 방식으로 매개변수화되며, 매개변수를 공유한다. 이는 SSM이 연속 시간 매개변수를 학습하기 때문에 중요한 차이점이다.
대부분의 SSM은 HiPPO 이론으로 초기화된 복소수 대각 행렬을 사용하며, 이러한 초기화가 SSM의 성공에 중요한 역할을 한다.

이를 바탕으로, SSM 계층을 RNN으로 교체하고 S4와 유사한 성능을 회복하기 위한 단계를 연구하였다.

Experimental setup

이 논문은 Long Range Arena 벤치마크(Tay et al., 2020)를 사용하여 장기 시퀀스 모델링 능력을 평가한다. 심층 SSM이 뛰어난 성능을 보여주었기 때문에, 이 벤치마크는 심층 RNN의 장기 모델링 능력을 탐구하는 데 적합하다.

실험은 6개의 계층을 가진 네트워크에서 SSM 계층을 RNN 계층으로 교체하여 진행하며, 각 실험은 세 번 반복되어 평균과 표준 오류를 보고한다. 네트워크는 AdamW 옵티마이저로 학습되며, 학습률과 하이퍼파라미터는 로그 그리드에서 조정된다.

Designing Performant Deep RNNs

이 섹션에서는 RNN이 LRA 벤치마크에서 심층 SSM과 유사한 성능을 내기 위해 필요한 단계를 설명한다. 서론에서 개요를 제시한 후, 각 단계는 실험적 증거와 이론적 고찰로 뒷받침된다.

Linear RNN layers are performant

이 연구의 주요 발견은 선형 RNN 계층이 비선형 MLP 또는 GLU와 결합될 때 매우 효과적이라는 점이다. 비선형성을 제거하고 단순히 $ x_k = A x_{k-1} + B u_k $로 계산하는 것만으로도 LRA 작업에서 성능이 향상되었다. 비록 선형 RNN의 성능이 S4보다 낮지만, 이 결과는 논문에서 비선형성을 제거할 동기를 제공한다. 이후 섹션에서는 선형 재귀의 장점을 활용해 학습 속도를 높이고, 장기 종속성을 학습하기 위한 초기화 및 정규화 방법을 제안한다. 텍스트와 검색 작업에서는 vanilla RNN이 깊은 SSM과 유사한 성능을 보인다.

결과는 비선형성이 RNN 성공의 핵심이라고 여겨지는 기존의 이론과 실제와는 달리, 선형 RNN 계층이 비선형 MLP 또는 GLU 블록과 결합될 때 효과적이라는 점을 보여준다. 깊은 모델에서 비선형성이 신호를 더 높은 주파수로 전달하여 시스템의 표현력을 높이고, 선형 RNN과 비선형 피드포워드 블록의 결합이 비선형 시스템을 잘 근사할 수 있음을 논의한다. 비선형 활성화는 학습 속도를 늦출 수 있다는 점도 강조된다.

Using complex diagonal recurrent matrices is eﬃcient

복소수 대각 행렬을 사용하여 깊은 선형 RNN의 학습과 추론 속도를 성능 저하 없이 크게 향상시킬 수 있음을 보여준다. 이 섹션에서는 Gupta et al. (2022a)의 DSS를 기반으로, Glorot 초기화된 선형 RNN의 초기화 스펙트럼에 맞춘 대각화된 버전을 구성하고, 초기화와 대각화가 성능에 미치는 영향을 분리하는 방법을 논의한다.

Linear RNN eigendecomposition

재귀 관계 $x_k = A x_{k-1} + B u_k$는 $x_{-1} = 0 \in \mathbb{R}^N$이라는 가정 하에 쉽게 전개할 수 있으며, 결과적으로:

$$ x_k = \sum_{j=0}^{k-1} A^j B u_{k-j} $$

행렬 $A$의 지수는 RNN에서 기울기 소실/폭주 문제를 유발한다. 비선형 RNN에서는 상태가 활성화 함수의 컴팩트 이미지에 제한되지만, 선형 RNN에서는 상태가 지수적으로 폭주하거나 소실될 수 있다. 이를 해결하기 위해, $A = P \Lambda P^{-1}$로 대각화할 수 있다. $ \bar{x}_k = \sum_{j=0}^{k-1} \Lambda^j \bar{B} u_{k-j} $ 여기서 $\bar{x}_k := P^{-1} x_k$ 및 $\bar{B} := P^{-1} B$이다. 출력 $y_k = \Re[\bar{C} \bar{x}_k] + D u_k$를 계산하고, $\Lambda, \bar{B}, \bar{C}$를 학습하면 성능을 유지하면서도 효율적으로 학습할 수 있다.

Are complex numbers really necessary? 대각화된 비대칭 행렬을 간편하게 표현하기 위해 복소수를 사용한다. 그러나 실수를 사용해서도 유사한 효율을 얻을 수 있다.

Stability. 타임스탬프 $k$에서 $\bar{x}_k$의 성분 $j$는 $|x_{k,j}| = O(|\lambda|^k)$로 진화한다. 따라서 안정성을 보장하려면 모든 $j$에 대해 $|\lambda_j| < 1$이어야 한다.

Learning in the diagonalized space

대각 형태의 순환 선형 시스템은 학습과 추론 속도를 크게 향상시킨다. 예를 들어, sCIFAR 구현에서 대각선 선형 RNN은 ReLU 기반 밀집 RNN보다 약 8배 빠르며, S4D 및 S5와 유사한 속도를 보여준다. 이는 대각 행렬의 거듭제곱 계산이 간단하고, 선형 재귀는 병렬화가 가능해 훈련 속도를 높이기 때문이다.

Equivalent initialization. 대각 선형 시스템의 이점을 초기화와 분리하기 위해, 밀집 선형 RNN과 비교 시 고유값 스펙트럼이 유지되는 초기화를 찾고자 하며, 이를 위해 랜덤 행렬 이론을 활용한다.

Theorem 3.1 $N \times N$ 실수 행렬 $A_N$이 평균 0, 분산 $ \frac{1}{N} $인 가우시안 항목들로 이루어질 때, $ N \to \infty $일수록 $ A_N $의 경험적 스펙트럼 $ \mu_N $은 원판 $ \lbrace |z| \leq 1 \rbrace \subset \mathbb{C} $ 상의 균일 확률 측도로 수렴한다.

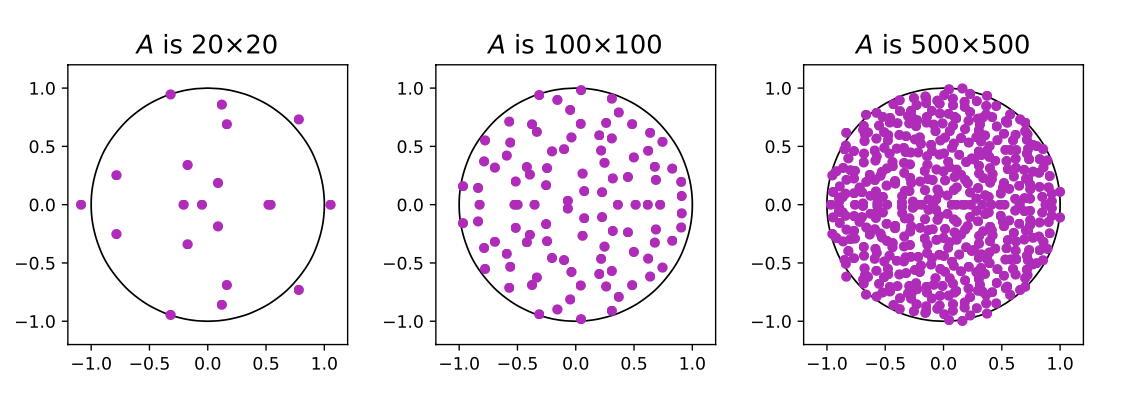
이 정리는 Glorot 초기화 시 행렬 $A$의 스펙트럼이 복소평면 $C$의 단위 원판에서 샘플링된다고 설명하며, 이는 Glorot 초기화가 안정적인 초기화를 제공해 선형 RNN 성능을 설명한다. 또한, Theorem 3.1에 따라 대각 시스템에서는 동일한 스펙트럼 초기화를 적용할 수 있으며, Λ는 단위 원판에서 균일하게 샘플링된 대각 행렬이어야 합니다. 복소수 지수 정의를 활용해, 반지름 $r_{\text{min}}$과 $r_{\text{max}}$ 사이의 고리에서 균일 샘플링하는 방식을 사용한다.

Lemma 3.2. 독립 균등 확률 변수 $ u_1, u_2 $와 $ 0 \leq r_{\text{min}} \leq r_{\text{max}} \leq 1 $을 사용하여 다음을 계산한다 $ \nu = -\frac{1}{2} \log\left(u_1 \left(r_{\text{max}}^2 - r_{\text{min}}^2\right) + r_{\text{min}}^2 \right) $, $ \theta = 2\pi u_2 $ 그런 다음 $ \exp(-\nu + i\theta) $는 복소평면에서 반지름 $ r_{\text{min}} $과 $ r_{\text{max}} $ 사이의 고리에서 균일하게 분포한다.

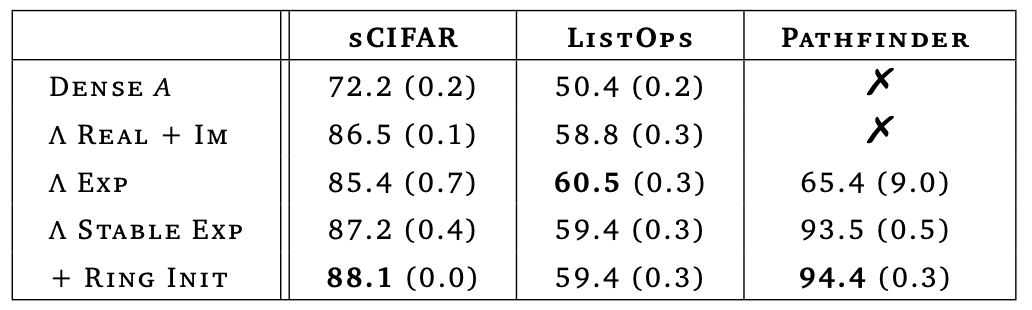
무한 너비에서 Glorot 초기화의 스펙트럼을 복원하려면 $ r_{\text{min}} = 0 $ 및 $ r_{\text{max}} = 1 $로 설정한다. 위 테이블은 복소수 대각 형태에서 깊은 선형 RNN을 학습한 결과를 보여준다. Λ의 대각 항목은 단위 원판에서 균일하게 초기화되며, $B$와 $C$는 Glorot 초기화가 적용된다. SSM 계산 후에는 신호의 실수 부분만 유지하고 허수 부분은 제거한다.

위 결과는 재귀를 대각화하면 ListOps 및 sCIFAR에서 정확도가 향상되고, 모든 LRA 작업에서 훈련 및 추론 시간이 크게 줄어들며, RNN이 S4D 및 S5와 같은 깊은 SSM만큼 빠르게 학습될 수 있음을 보여준다.

Benefits of stable exponential parameterization

복소수 대각 재귀가 계산적으로 효율적이지만, 학습이 불안정할 수 있음을 보여주었다. 장기 의존성을 학습하려면 고유값이 1에 가까워야 하지만, 이는 시스템을 불안정하게 만들 수 있다. 이 섹션에서는 RNN의 안정적인 파라미터화와 $ r_{\text{min}} $ 및 $ r_{\text{max}} $ 조정의 이점을 설명한다.

Optimization under exponential parameterization. Lemma 3.2는 대각화된 RNN의 파라미터화를 $\Lambda = \text{diag}(\exp(-\nu + i\theta))$로 제안하며, 여기서 $\nu$와 $\theta$는 학습 가능한 파라미터이다. 이 방법은 크기와 주파수를 분리하여 Adam 최적화를 용이하게 하며, ZOH 이산화와 유사한 특징을 가지며 PathFinder의 성능을 향상시킨다.

Enforcing stability. 지수 파라미터화는 고유값의 안정성을 쉽게 보장할 수 있다. 초기화 시 $|\lambda_j| \leq 1$이므로, 학습 중에는 $\lambda_j := \exp(-\exp(\nu_{\text{log}}) + i\theta_j)$를 사용하여 안정성을 유지한다. 이는 $|\lambda| = 1$ 주변의 세밀한 조정을 가능하게 하며, 대부분의 LRA 작업에서 유용하다.

안정적인 파라미터화의 이점은 Λ의 고유값을 단위 원판에 가까운 고리에서 초기화하여 장기 상호작용을 촉진하고 기울기 소멸을 방지하는 것이다. Gu et al. (2022b) 및 Gupta et al. (2022a)에 따르면, 고유값의 크기가 1에 가까워야 먼 토큰 간의 상호작용을 잘 처리할 수 있다. 안정성을 보장하면 $ r_{\text{max}} $을 0.99까지 증가시켜 성능을 향상시킬 수 있다. 다른 작업에서도 유사한 이점을 확인할 수 있으며, 작은 위상의 고유값 초기화가 장기 추론 작업에 유용하다.

Additional considerations for long-range reasoning tasks

지금까지 모델은 PathX(16𝑘 토큰 길이의 가장 어려운 데이터셋)를 학습하지 못하였다. 이 섹션에서는 긴 범위 의존성을 학습하기 위한 추가 수정 사항과 최종 LRU 모델 완성 방법을 논의한다.

Normalization. Λ의 고유값을 단위 원판에 가깝게 초기화했으나, $ r_{\text{min}} $과 $ r_{\text{max}} $을 1에 가까워지게 하면서 초기화 시 학습 손실이 급격히 증가하였다. 이 섹션에서는 이 현상을 설명하고, 문제 해결 및 성능 향상을 위한 숨겨진 활성화의 정규화 방법을 제시한다.

Proposition 3.3 Λ가 복소평면에서 반지름 $ r_{\text{min}} < r_{\text{max}} < 1 $ 사이의 고리에서 균일하게 샘플링된 고유값을 가지는 대각 행렬일 때, 상수 입력 또는 백색 잡음 입력과 Glorot 입력 투영 하에서 상태 $ x_k $의 제곱 노름은 $ k \to \infty $에서 다음과 같이 수렴한다:

$$ \mathbb{E}[||x_\infty||^2_2] = \frac{1}{r_{\text{max}}^2 - r_{\text{min}}^2} \log \left(\frac{1 - r_{\text{min}}^2}{1 - r_{\text{max}}^2}\right) \mathbb{E}[||B u||^2_2] $$

이 결과는 $ r_{\text{min}} = r_{\text{max}} = r $일 때, 단위 원판에 $ \rho $-가까운 값으로 초기화하면 순전파가 $ 1/\rho $만큼 폭발한다는 것이다. 여기서 $ \epsilon = r_{\text{max}} - r_{\text{min}} $ 및 $ \rho = 1 - r_{\text{max}} $로 두면, 다음과 같은 극한 결과를 얻는다:

$$ \lim_{\epsilon \to 0} \frac{\mathbb{E}[||x_\infty||^2_2]}{\mathbb{E}[||B u||^2_2]} = \lim_{\epsilon \to 0} \big[ \frac{1}{\epsilon} \log \big( 1 + \frac{\epsilon}{p} \big) \big] = \lim_{\epsilon \to 0} \big[ \frac{1}{\epsilon} \big( \frac{\epsilon}{p} + O(\epsilon^2) \big) \big] = \frac{1}{p} = \frac{1}{1 - r^2} $$

순전파를 위한 효과적인 정규화 방안을 도출하기 위해, 백색 잡음 입력 하에서 1/𝜌 이득 공식의 단순화된 유도 과정을 제시한다. 1차원 설정을 고려할 때, Λ = 𝜆 ∈ C이고 𝐵 = 1이라고 가정한다. p^* )는 ( p \in C )의 켤레를 나타냅니다. 우리는 (|p|^2 = p^*p)로, 입력에 대한 기댓값을 사용하여 Eq.(4)와 ( \mathbb{E}[u_{k-i}u_{k-j}] = 0 ) (여기서 ( i \neq j ))를 고려하면:

$$ \mathbb{E}|x_k|^2 = \big( \sum_{i=0}^{k-1} \lambda^i \mathbb{E}[u_{k - i}] \big) \big( \sum_{j=0}^{k-1} \lambda^j \mathbb{E}[u_{k - j}] \big)^* = \sum_{i,j=0}^{k-1} \lambda^i(\lambda^j) \mathbb{E}[u_{k - i} u_{k - j}] = \sum_{i=0}^{k-1} |\lambda|^{2i} \overset{\infty}{\rightarrow} \frac{1}{1 - |\lambda|^2} $$

여기서 $\lambda$가 단위 원판의 가장자리에 가까운 경우 $\mathbb{E}[|x|^2] \approx \frac{1}{1 - |\lambda|^2}$로 수렴한다.

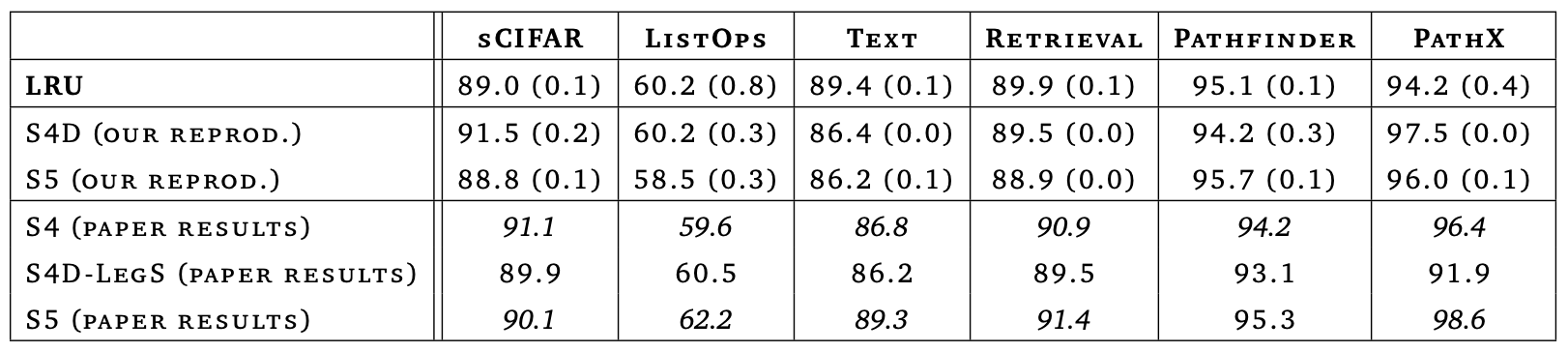
정규화 파라미터 $\gamma_{\text{log}} \in \mathbb{R}^N$를 $\log(\sqrt{1 - |\lambda_i|^2})$로 초기화하고, 재귀식을 다음과 같이 수정한다:

$$ x_k = \Lambda x_{k-1} + \exp(\gamma_{\text{log}}) \odot (B u_k), $$

여기서 $\odot$는 원소별 곱이다. 이 $\gamma$ 정규화는 RNN이 입력을 적절히 조정하게 하고, sCIFAR와 Pathfinder와 같은 작업에서 성능을 일관되게 향상시킨다.

Reducing Eigenvalue Phase at Initialization. 대각화된 재귀에서 $\Lambda = \text{diag}(\exp(-\exp(\nu_{\text{log}}) + \theta))$로 설정한다. 여기서 $\nu_{\text{log}}$는 고유값의 로그 크기 벡터, $\theta$는 위상 벡터이다. 긴 시퀀스에서 $\theta$를 균일하게 $[0, 2\pi]$로 초기화하면 많은 진동이 발생하며, 이는 장기 의존성과는 별개로 RNN이 저장하는 정보의 본질과 관련이 있다. 이로 인해 네트워크가 허위 특성을 학습할 수 있으며, PathX에서는 학습 손실이 하위 최적의 최소화기로 수렴한다. 이를 해결하기 위해 $\theta$의 범위를 0 주변으로 제한하고, $\theta$를 로그 스케일로 파라미터화하여 최적화를 돕는다.

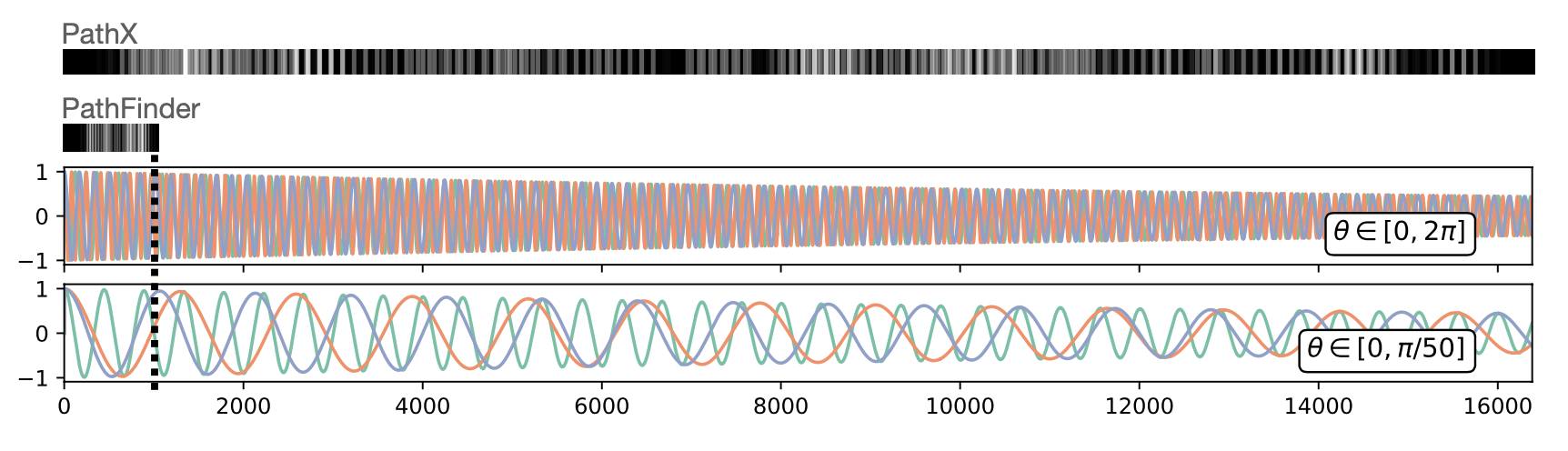
초기화 시 위상을 [0, $ \pi/10 $]로 제한한 결과, 우리의 LRU는 PathX에서 94.2%를 달성하였다. 𝛾 정규화와 위상 제한은 PathX 해결에 필수적이었으며, 위상 제한만으로는 학습이 어려웠다.

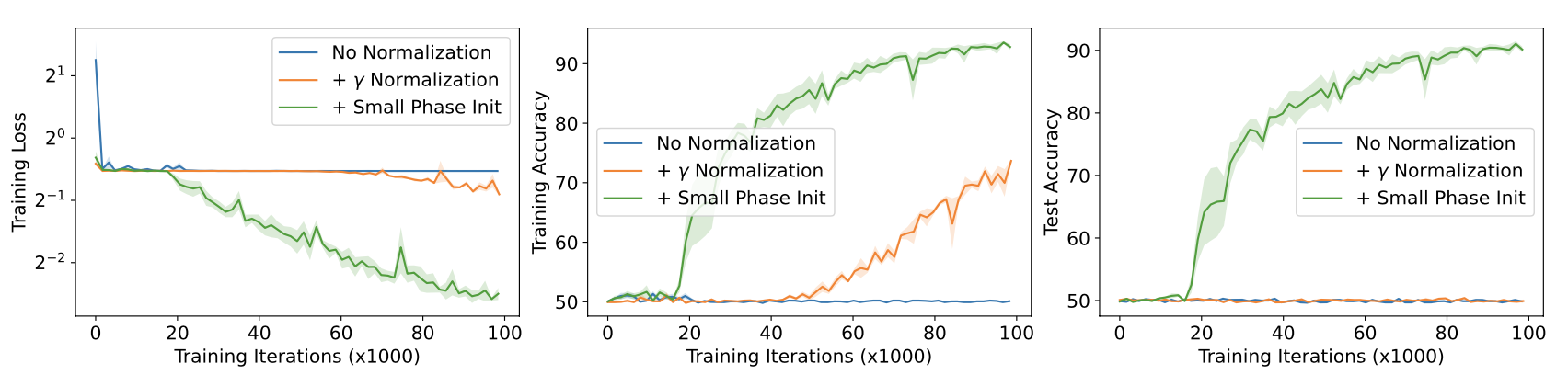
모든 구성 요소를 종합하여 새로운 모델을 선형 재귀 유닛(Linear Recurrent Unit, LRU)이라 명명한다. LRU는 깊은 RNN을 효율적으로 초기화하고 학습할 수 있는 유연하고 해석 가능한 프레임워크를 제공하며, 모든 LRA 작업에서 깊은 상태 공간 모델과 같은 성능과 효율성을 보여준다.

Insights on S4 and Variants

이 섹션에서는 LRU 모델과 대각 SSM의 유사점과 차이점을 살펴보고, 주요 통찰을 제공한다.

대각 상태 공간 모델(DSS, S4D, S5)은 연속 시간 모델을 이산화하여 파라미터화된다. 이산화는 다음 재귀식으로 이어진다. $x_k = \exp(\Delta \tilde{A}) x_{k-1} + (\exp(\Delta \tilde{A}) - I) \tilde{A}^{-1} \tilde{B} u_k $

Matrix exponentials make training easier. ZOH 공식에서 지수 함수는 정확한 적분에 기인하며, $ x_{ct}(\Delta k) = \exp(\Delta \tilde{A}) x_{ct}(\Delta (k - 1)) $로 이어진다. S4에서 영감을 받은 모델은 안정성을 위해 𝐴의 실수 부분을 비선형성에 통합합니다. 그러나 지수 파라미터화의 이점은 정확한 적분보다는 크기-위상 분리와 대각화된 공간에서 학습의 장점에서 비롯되며, 비선형성을 추가하는 것이 유익하다는 것도 실험에서 확인되었다.

Structured initialization is not necessary. Gu et al. (2022a), Gupta et al. (2022b), 및 Smith et al. (2022)은 HiPPO 구조에서 벗어난 𝐴의 초기화에 대해 논의했지만, 이 연구는 단위 원판의 슬라이스에서의 균일 초기화와 적절한 정규화만으로 PathX를 해결할 수 있음을 처음으로 보여주었다. 균일 초기화는 복잡한 상태 공간 모델과 유사한 성능을 발휘하며, HiPPO 이론이 S4의 주요 성공 원천이라고 보기 어렵다는 것을 시사한다.

Discretization changes initialization spectrum. S4D-Lin에서는 $ A = \text{diag}(\tilde{a}) $로 초기화되며, 고유값은 $ \exp(-\Delta/2 + i\pi \Delta n) $로 설정된다. 예를 들어, $ \Delta = 1 \times 10^{-3} $, $ N = 128 $일 때, 고유값의 크기는 약 0.9995이고, 위상은 [0, $\pi/8$] 범위이다. 위 결과에 따르면, 고유값의 위상과 크기를 연결할 필요 없이 좋은 성능을 달성할 수 있으며, 전체 고리에서의 초기화가 효과적이다. 초기화 위상을 0 근처로 조정하는 것은 긴 시퀀스에만 필요하며, S4에서 이미 반영되어 있다. 이 연구의 결과는 Δ 파라미터를 통한 실수와 허수 부분의 연결이 성능에 필수적이지 않음을 보여준다.

Discretization performs normalization. 이 연구의 모델과 ZOH-이산화된 S4의 주요 차이는 입력 $ u_k $에 대한 행렬 승수 $(\exp(\Delta \tilde{A}) - I) \tilde{A}^{-1} \tilde{B}$에서 나타난다. S4D에서 이 승수를 $\Delta \tilde{B}$로 간단히 교체해도 성능이 비슷하게 유지됨을 발견하였다. 재귀식은 다음과 같다. $ x_k = \exp(\Delta \tilde{a}) x_{k-1} + \Delta \tilde{1}_N u_k $ 이 재귀식은 $ \Delta $ 승수가 폭주를 방지하는 데 효과적이며, 이는 $\gamma$ 정규화 인자와 유사하다.

Parameter sharing is not necessary. 이산화 과정에서 Δ가 $ \tilde{A} $와 $ \tilde{B} $에 곱해져 학습 중 결합되지만, 이를 별도 파라미터로 분리해도 성능이 유지된다. 이는 ODE 이산화 관점이 S4 성능에 필수적이지 않음을 시사한다.

이 논의에서, 상태 공간 모델의 성공은 선형 재귀와 대각선 지수 행렬, 그리고 이산화로 인한 정규화와 초기화 덕분이라는 결론을 내릴 수 있다. 파라미터 공유나 연속 시간 해석 같은 이산화의 부수적 요소는 성능에 큰 영향을 미치지 않는다.

Conclusion

이 논문에서는 선형 재귀 유닛(LRU)이라는 새로운 RNN 레이어를 소개하고, 이를 깊은 시퀀스 모델의 핵심 레이어로 효과적으로 활용할 수 있음을 보여준다. vanilla RNN의 선형화, 대각화, 지수 파라미터화 및 정규화 등의 수정을 통해 성능을 크게 향상시킨다. 이 연구의 모델은 현대의 깊은 상태 공간 모델들과 유사한 성능을 보이지만, 연속 시간 시스템의 이산화나 구조화된 전이 행렬에 의존하지 않는다. 대신, Glorot 초기화와 표준 딥러닝 분석을 기반으로 개선된 성능을 제공한다.

LRU

Resurrecting Recurrent Neural Networks for Long Sequences